Here's some more in depth analysis of one pole filters which we need later on to create more complex models. I'm dividing this article into several sections. First we'll present a "workable" schematic that lets us handle single pole lowpass filters with a lot of flexibility. Then we'll introduce the concept of non-linearities i.e. distortion within a single lowpass filter. Latter is important if we want to understand why one can't make a linear filter sound analogue with separate distortion sections before or after it. In a subsequent article we'll get our hands dirty with code, with a special focus on strategies to solve the non-linear properties.

Did you know?

• one pole filters can have separate inputs for lowpass and highpass outputs
• active one pole filters can essentially have an additional inverting lowpass input
• despite the tanh() terms of the active lowpass, the output is not bound to +/- 1

eye candy

Here's a schematic with a bunch of simplifications and ingredients that help us model a lowpass filter e.g. as used in a transistor ladder or a OTA cascade configuration (more on the difference later):

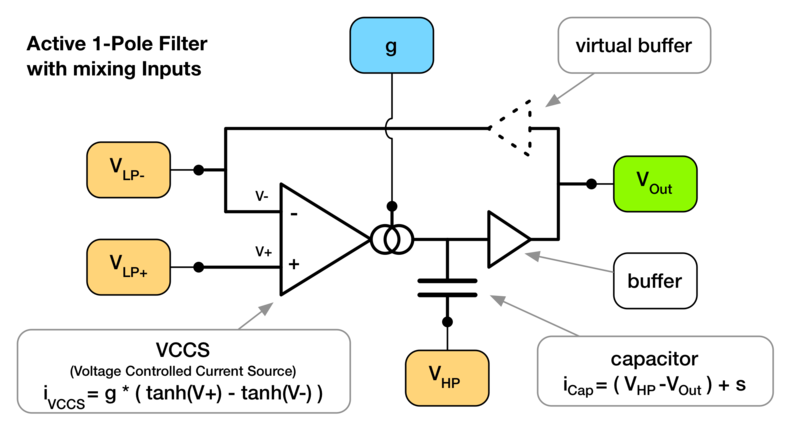
I'm sure most people who deal with filter models have already seen and understood the theory behind one pole lowpass filters. You can either believe me or read the Cytomic paper when I say that the linear approximation of an active lowpass leads to the same equations as that of a RC filter. Let's assume the capacitor is connected to ground (V=0) and the inverting LP input isn't connected, we'll get exactly the same equation Vout = ( g * Vin + s ) / ( g + 1 ) as in our RC example.

The first thing to note is that I have chosen a component labelled "VCCS". In the first version of this article this was an OTA, but I got the equation wrong. Fixing this would have made this tutorial either too complex, or the filter model too inflexible. However, by choosing a more general component as Voltage Controlled Current Source with separately non-linear inputs that's merely a concept than an actual part, we get a building block that's both useful for modeling transistor ladders and OTA cascades and explains the technique. To illustrate the trick, here are the formulas for active one pole filters in comparison:

OTA: Iota = g * tanh(V+ - V-) with simple circuit schematic
Transistor ladder: Itl = g * ( tanh(V+) - tanh(V-) ) with rather complex schematic
VCCS: Ivccs = g * ( tanh(V+) - tanh(V-) ) with simple schematic

The second thing you should notice is the inverting lowpass input. The reason this works (even in case of the simple OTA based circuit) is because there's a virtual buffer between the filter's output and the negative coupling input of the Amplifier. That virtual buffer is a set of resistors (typically in the vicinity of 100k) in real OTA circuits which surround the circuitry but have no effect on the actual math. They do however minimize the feed forward from the inverting input to Vout by a considerable factor so that no audible signal can bleed through. Hence we can treat these resistors virtually as a buffer between our filter output and the negative port of the VCCS (which in this case behaves exactly like an actual OTA). This makes our active lowpass filter unlike a RC filter even if we assume linear approximations.

So, let's do the math for the linear case!

currents:
Ivccs = g * ( Vlp - (Vout + Vln) )
Icap = (Vout - Vhp) + s

KCL:

0 = Ivccs - Icap
0 = g * ( Vlp - (Vout + Vln) ) - (Vout - Vhp) + s

hence: Vout = (-Vln*g+Vlp*g+Vhp+s)/(g+1)

Where Vlp is the non-inverting lowpass input, Vln is the invertig one and Vhp is the highpass input. Then, for trapezoidal integration we get the following update for s for the next sample step:

s[n+1] = 2*(Vout[n]-Vhp[n]) - s[n]

Let's also not forget that g = tan(PI * cutoff/samplerate), which makes this all that's needed to compute this active input-mixing lowpass filter as a linear approximation.

make it scream!

I won't explain this now, but there's a reason that analogue filters sound great while digital filters usually don't. If you want an eye opener, read Dave Rossum's (of E-mu fame) paper Making Digital Filters sound Analog - it shows that people have always wanted that sound and it shows that it always had to be achieved by saturation inside the filter. It furthermore explains that the best way to achieve it would be doing what circuit simulators do. Which is pretty much what we're presenting here, at least to some nice enough degree.

I guess you've already noticed the tanh() terms in above schematic:

Ivccs = g * ( tanh(V+) - tanh(V-) )

So there they are. The muchly fabled tanh() terms that add non-linear behaviour to our filter, embedded somewhere inside our VCCS component which acts as our voltage controlled resistor. I think it would exceed the scope of this article if I went through all the citations needed to explain where those tanh() terms come from. For the sake of simplicity, let's just assume that those waveshapers are a reasonably good approximation to the non-linear effects inside the actual parts (differential transistor pairs, OTAs etc., with their respective placements).

In order to add non-linearities to our equations we simply add the non-linear terms. KCL still applies, and only because the "conductance" changes in respect to the input voltage, there's no change in the equations derived from the currents. Let's start with a simple lowpass and add the additional inputs later:

linear lowpass version: Vout = g * (Vin - Vout) + s
non-linear version: Vout = g * ( tanh(Vin) - tanh(Vout) ) + s

Note that I kept the equations in their implicit form. If I added array indices to the variables, all off them would read [n]. The reason for the implicit form being, while we can solve the linear equation for Vout, we can not do so for the non-linear one. It's not possible to isolate Vout on one side because we can't somehow divide by a constant to get rid of the enclosing tanh() term.

This can do one's heads in. Apart from the obvious strategy to use Euler's Method for integration - and thus use tanh( Vout[n-1] ) - people might feel compelled to let the negative coupling feedback be linear. If we do so, we arrive at this neatly solvable equation:

Vout = g * ( tanh(Vin) -Vout ) + s // <-- don't do this

However, with this equation Vout is always bound to +/- 1, because obviously the input will never exceed +1 or -1. Even if Vin is constantly set to +5, Vout will always ever reach tanh(5) which will always be below 1 ... But then, consider a constant input of +5 in this case:

Vout = g * ( tanh(Vin) - tanh(Vout) ) + s
s updated for next iteration: s = 2 * Vout - s

In this case Vout (and s) will settle at +5! That is because the damping factor in the negative coupling is smaller than the output and thus the output can grow beyond the limits of the (waveshaped) input. You don't believe it? A very simple test can confirm that this is the only solution, if we calculate a sample step. We assume Vin = +5, Vout = +5, s = +5, 0 < g < 1 and put them into above formula:

5 = g * ( tanh(5)-tanh(5) ) + 5
s = 2*5 - 5

If you're still not convinced, just do the experiment with the code I'll post later. Feed those equations a constant signal beyond +1 and see how the output isn't bounded!

The gist being, an active non-linear lowpass filter is not bounded to +/- 1 even if tanh() waveshapers are modeled inside. That's an important notion for the design of complex filters such as cascades, sallen-keys and ladders. The generally higher output gain of this kind of filter sounds considerably different due to gain staging of subsequent filter stages!

input mixing non-linear one pole filter

Now, let's have a look at our implicit equation for the full filter model:

Vout[n] = g * ( tanh( Vlp[n] ) - tanh( Vout[n] + Vln[n] ) ) + Vhp[n] + s[n]
s[n+1] = 2 * ( Vout[n] - Vhp[n] ) - s[n]

Some trivia about it:

• the non-inverting lowpass gets shaped separately from the feedback, as expected from, say, a transistor ladder
• the inverting lowpass input gets waveshaped with the feedback. This not just results in an inverting lowpass but also in a different sound! With this input you get the distoriton bahaviour of OTA based filters
• the highpass configuration only gets waveshaped in the feedback, the feed forward is linear

Why do we need this? - A transistor ladder filter can essentially be modeled using a cascade of these one pole stages connected by the non-inverting lowpass inputs. This might for instance be the case with the SSM 2044 filter chip which poses a ladder configuration (I'll measure this out one day). Most all-in-one-chip filter circuits however, such as those using the OTA-based CEM3320 or SSM2040 chips connect each stage via the inverting lowpass input. Latter can be configured for highpass stages, as found in the ELKA Synthex. If you want to model those filters, understanding this one pole filter might be a good start.

Solving its implicit equation works many ways... I'll post an extra article on this!

---

*Update Feb 27th:I was made aware that the equation used for the differential amplifier was not correct for an OTA output current. In order to keep the tutorial simple and the filter flexible, I have chosen to introduce a conceptual part VCCS which poses a Voltage Controlled Current Source. This trick lets us stick to the more flexible formula, but doesn't change the use case for OTA cascades (which I wish to introduce in future tutorials). On the downside this tutorial is a little less authentic, but that's IMHO better than either presenting a lesser solution or a harder to understand structure. I hope to show the difference to actual (authentic) components in a subsequent article. This update also fixed a typo in one of the equations.